Janez and I have recently returned from a two-week stay in Moscow, Russian Federation, where we were teaching data mining to MA students of Applied Statistics. This is a new Master’s course that attracts the best students from different backgrounds and teaches them statistical methods for work in the industry.

It was a real pleasure working at HSE. The students were proactive by asking questions and really challenged us to do our best.

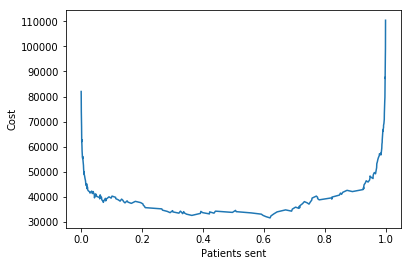
One of the things we did was compute minimum cost of misclassifications. The story goes like this. Sara is a doctor and has data on 303 patients with heart disease (Orange’s heart-disease.tab data set). She used some classifiers and now has to decide how many patients to send for further tests. Naive Bayes classifier, for example, returned probabilities of a patient being sick (column Naive Bayes 1). For each threshold in probabilites, she will compute how many false positives (patients declared sick when healthy) and how many false negatives (patients declared healthy when sick) a classifiers returns. Each mistake is associated with a cost. Now she wants to find out, how many patients to send for tests (what probability threshold to choose) so that her cost is the lowest.

First, import all the libraries we will need:

import matplotlib.pyplot as plt
import numpy as np

from Orange.data import Table
from Orange.classification import NaiveBayesLearner, TreeLearner
from Orange.evaluation import CrossValidation

Then load heart disease data (and print a sample).

heart = Table("heart_disease")
print(heart[:5])

Now, train classifiers and select probabilities of Naive Bayes for a patient being sick.

scores = CrossValidation(heart, [NaiveBayesLearner(), TreeLearner()])

#take probabilites of class 1 (sick) of NaiveBayesLearner
p1 = scores.probabilities[0][:, 1]

#take actual class values
y = scores.actual

#cost of false positive (patient classified as sick when healthy)
fp_cost = 500

#cost of false negative (patient classified as healthy when sick)
fn_cost = 800

Set counts, where we declare 0 patients being sick (threshold >1).

fp = 0
#start with threshold above 1 (no one is sick)
fn = np.sum(y)

For each threshold, compute the cost associated with each type of mistake.

ps = []
costs = []

#compute costs of classifying i patients as sick
for i in np.argsort(p1)[::-1]:
    if y[i] == 0:
        fp += 1
    else:
        fn -= 1
    ps.append(p1[i])
    costs.append(fp * fp_cost + fn * fn_cost)

In the end, we get a list of probability thresholds and associated costs. Now let us find the minimum cost and its probability of a patient being sick.

costs = np.array(costs)
#find probability of a patient being sick at lowest cost
print(ps[costs.argmin()])

This means the threshold that minimizes our cost for a given classifier is 0.620655. Sara would send all the patients with a probability of being sick higher or equal than 0.620655  for further tests.

At the end, we can also plot the cost to patients sent curve.

fig, ax = plt.subplots()
plt.plot(ps, costs)
ax.set_xlabel('Patients sent')
ax.set_ylabel('Cost')

You can download the IPython Notebook here: [download id=“2053”].