This is a guest blog from the Google Summer of Code project.

Gradient Descent was implemented as a part of my Google Summer of Code project and it is available in the Orange3-Educational add-on. It simulates gradient descent for either Logistic or Linear regression, depending on the type of the input data. Gradient descent is iterative approach to optimize model parameters that minimize the cost function. In machine learning, the cost function corresponds to prediction error when the model is used on the training data set.

Gradient Descent widget takes data on input and outputs the model and its coefficients.

The widget displays the value of the cost function given two parameters of the model. For linear regression, we consider feature from the training set with the parameters being the intercept and the slope. For logistic regression, the widget considers two feature and their associated multiplicative parameters, setting the intercept to zero. Screenshot bellow shows gradient descent on a Iris data set, where we consider petal length and sepal width on the input and predict the probability that iris comes from the family of Iris versicolor.

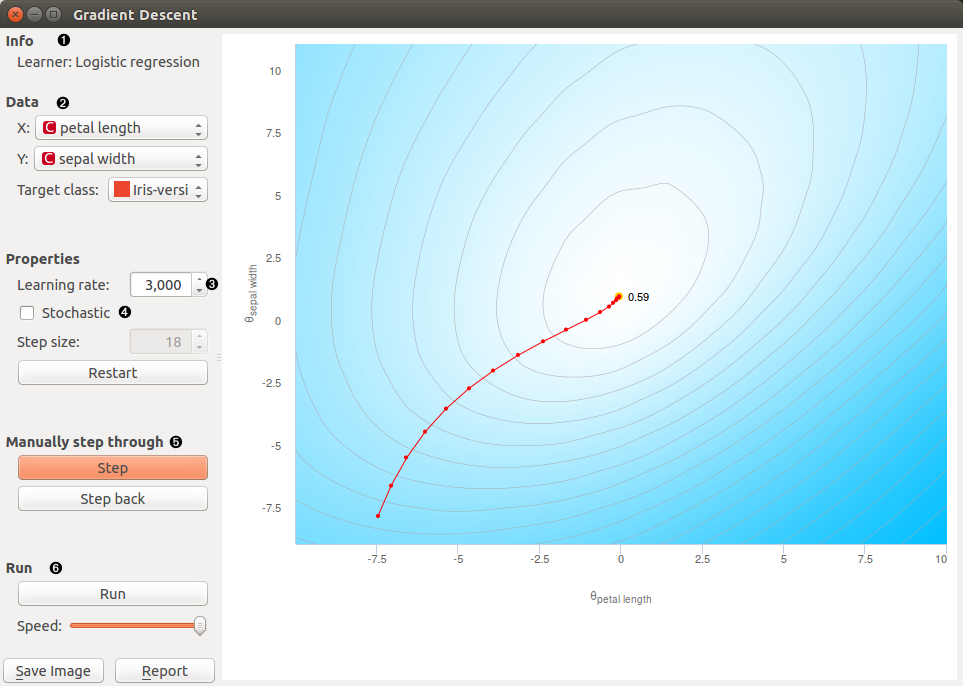
1. The type of the model used (either Logistic regression or Linear regression)
2. Input features (one for X and one for Y axis) and the target class
3. Learning rate is the step size of the gradient descent
4. In a single iteration step, stochastic approach considers only a single data instance (instead of entire training set). Convergence in terms of iterations steps is slower, and we can instruct the widget to display the progress of optimization only after given number of steps (Step size)
5. Step through the algorithm (steps can be reverted with step back button)
6. Run optimization until convergence

Following shows gradient descent for linear regression using The Boston Housing Data Set when trying to predict the median value of a house given its age.

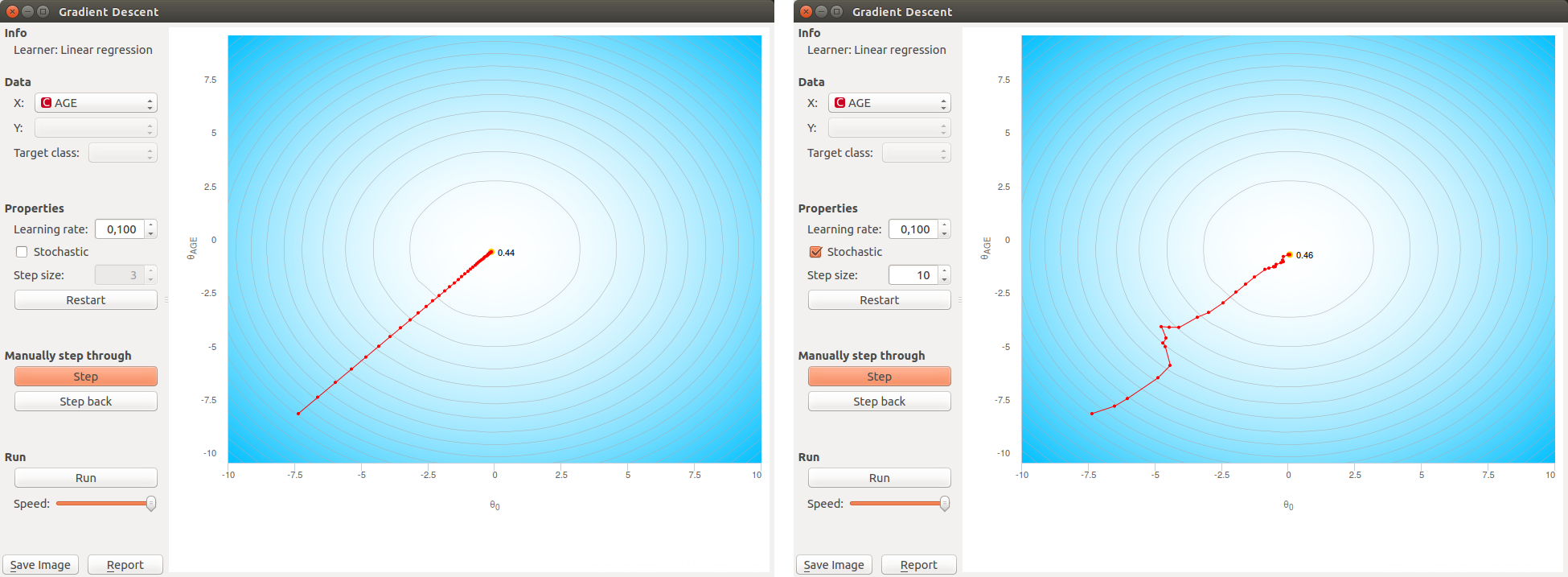
On the left we use the regular and on the right the stochastic gradient descent. While the regular descent goes straight to the target, the path of stochastic is not as smooth.

We can use the widget to simulate some dangerous, unwanted behavior of gradient descent. The following screenshots show two extreme cases with too high learning rate where optimization function never converges, and a low learning rate where convergence is painfully slow.

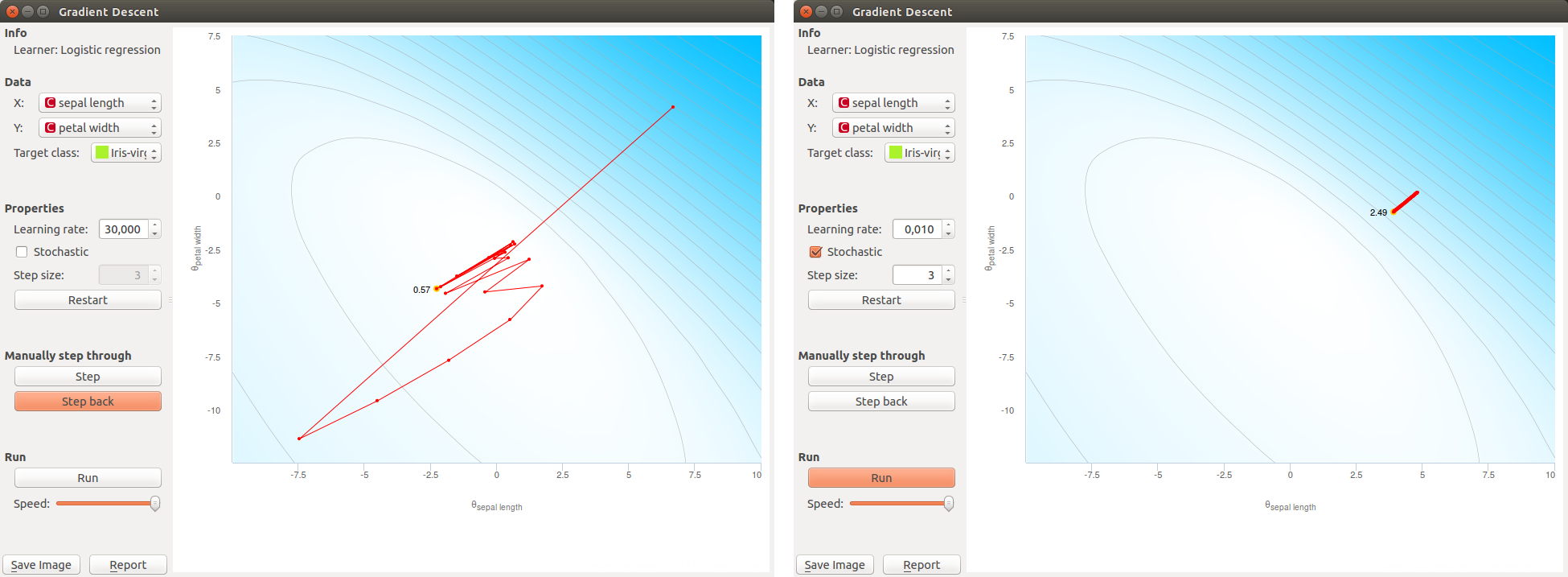
The two problems as illustrated above are the reason that many implementations of numerical optimization use adaptive learning rates. We can simulate this in the widget by modifying the learning rate for each step of the optimization.